一道数学题|A Math Problem

发表于 更新于 Waline： 阅读次数： 本文字数： 1.3k 阅读时长 ≈ 1 分钟

一天遇到了一道题
点击图片查看大图

思考半天也不知道第三小问怎么做，幸好首项只有36种可能，枚举了[1,17]中的奇数就算出了答案，老师讲评时也用了枚举法算的，还画出了这幅图，让我有了一种图论题的感觉。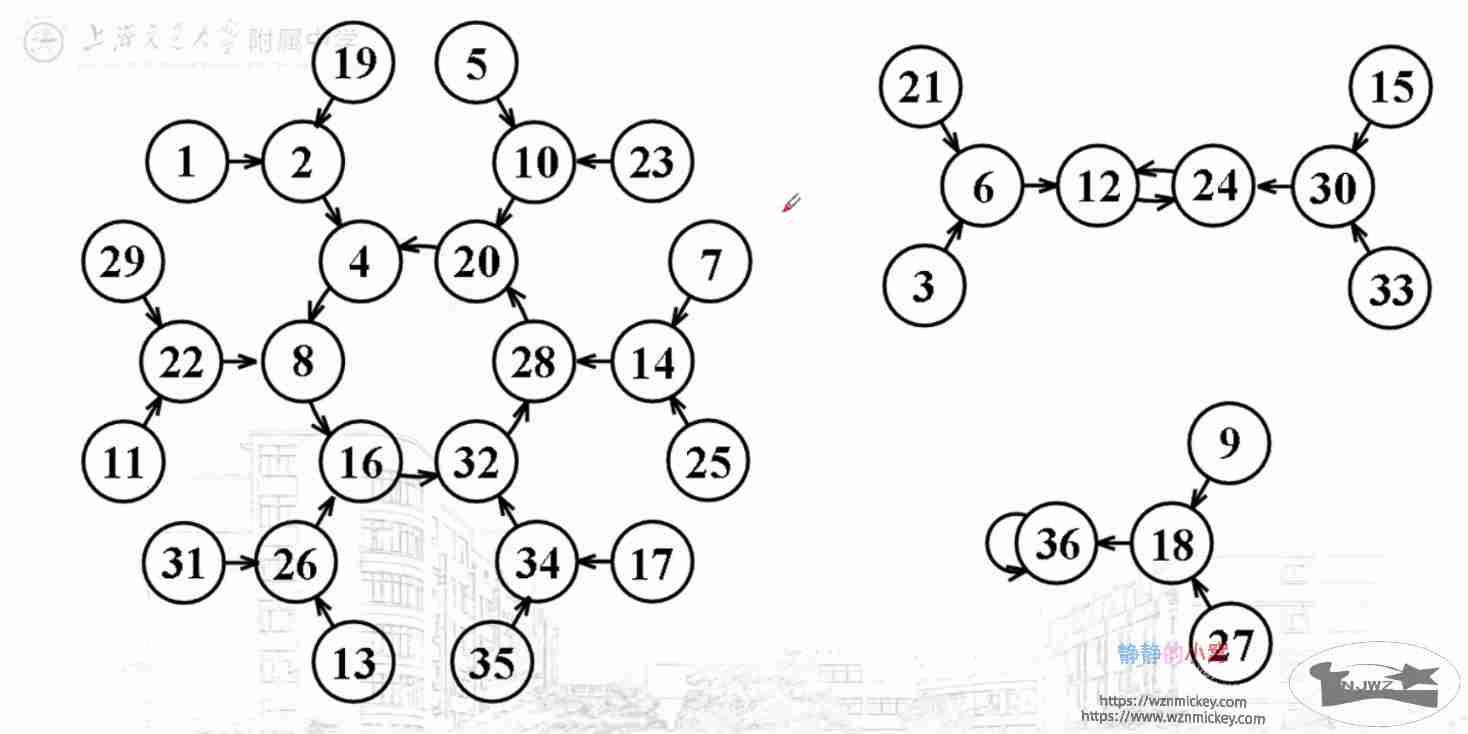

老师又让我们思考36改为其他数值的情况，然而我并不能想出来，又想到仿佛可以用图的方法做，于是就写了一段算了一下。结果如下：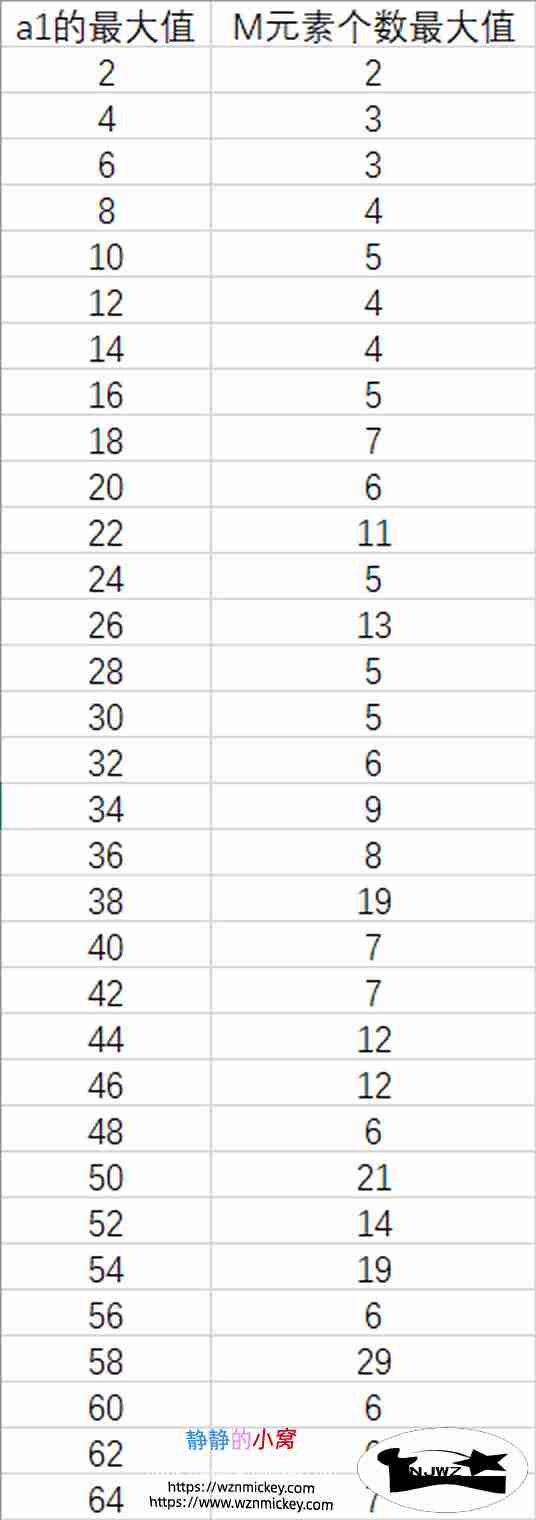

这有什么规律吗？去问了老师，结果老师回复

是我想太多了。

好久没做过题了，也比较懒，数据量也不大，就比较暴力了，代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
int main()
{
/*
a₁<=2x,
aₙ₊₁= 2aₙ, 　　aₙ<=x
　　　2aₙ-2x , aₙ>x
题目中x=18
*/
	int a[260][260];
	int m;
	for (int x=1;x<=100;x++)//aₙ的最大值为2x
	{
		int ans=0;
		for (int i=1;i<=255;i++)
			for (int j=1;j<=255;j++)
				a[i][j]=1000;//初始化
		for (int i=1;i<=2*x;i++)//aₙ₋₁的值为i
		{
			//计算aₙ的值
			int j;
			if (i<=x) j=2*i;
			else j=2*i-2*x;
			a[i][j]=1;
		}
		//算边
		for (int i=1;i<=2*x;i++)
		{
			for (int j=1;j<=2*x;j++)
			{
				for (int k=1;k<=2*x;k++)
				{
					a[j][k]=min(a[j][k],a[j][i]+a[i][k]);
				}
			}
		}
		//计算元素最大个数
		for (int i=1;i<=2*x;i++)
		{
			for (int j=1;j<=2*x;j++)
			{
				if (a[i][j]!=1000) ans=max(ans,a[i][j]);
			}
		}
		ans++;//点数=边数+1
		m=2*x;
		printf("%d %d\n",m,ans);
	}
	return 0;
}

解答最后有这么一段话：

事实上，规律是：
首项是整数时，第二项是偶数，第三项是4的倍数，任意一项不超过36
(1) 如果首项是3的倍数，那么由第二问的结论，每一项都是3的倍数，那么第三项是12的倍数，只能是12或24或36，于是由递推关系，第三项起最多2项，考虑前两项，M的元素最多4个，实际上M的元素个数可能是1或2或3或4
(2) 如果首项不是3的倍数，则M中的元素均不是3的倍数，所以第三项可能是4、8、16、20、28、32其中一项，那么以后形成这6项之间的循环，于是考虑前两项，M中元素最多8项，实际上M的元素个数可能是6或7或8
综上，M的元素个数最多为8个，当首项为1或5或7或11或13或17或19或23或25或29或31或35时取到。