拜登会团结美国吗|Will Biden unite the USA?
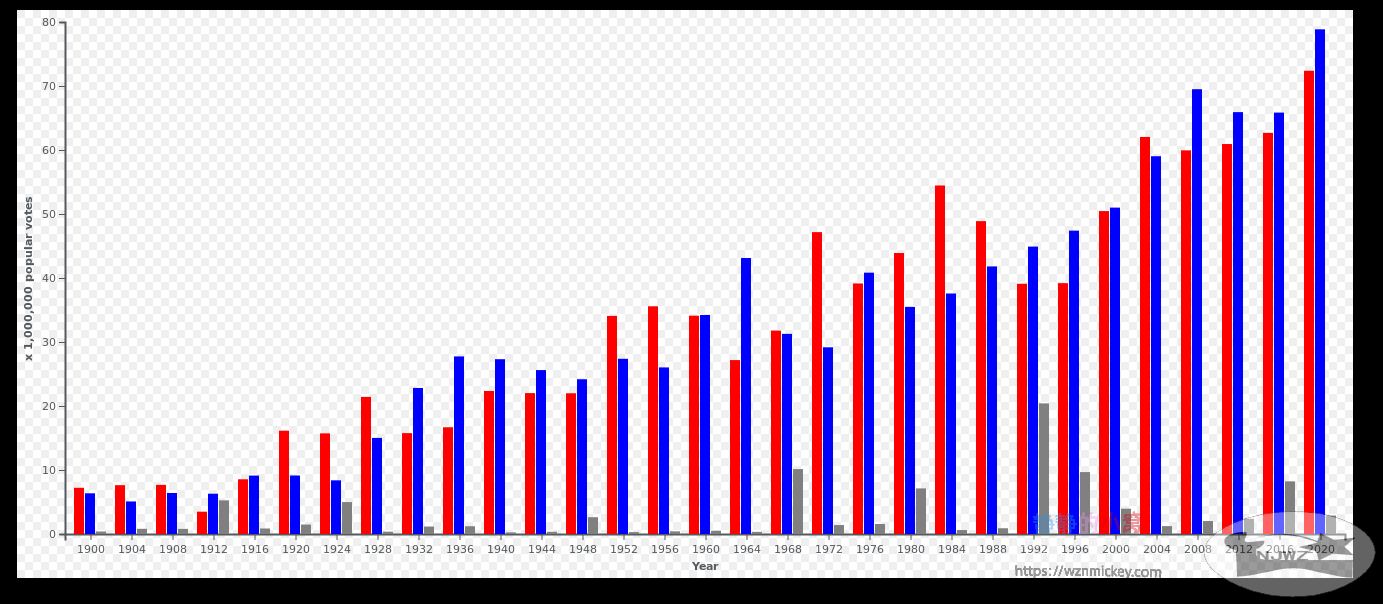
不管各方如何看待这场选举,有一点是各方都认可的,即特朗普的支持者数量没有减少。这次选举中双方并不是以从对方手中获取摇摆的选民作为目标,而是将获取之前没有参与选举的选民作为了目标。这也就使得拜登在普选票上的获胜(特朗普所称的选举作弊主要体现在摇摆州的少数几十万张票,不会涉及拜登普选票超过特朗普这一事)并不意味着将大量原本特朗普的支持者变为自己的支持者,也很难说特朗普的支持者的支持拜登的倾向会有增加。
选举的这种情况并非是二位候选人的有意为之,而是源于美国民众在众多观点的巨大分歧导致的,偏向中间所获得的选民远比不上更加极端政策激发出的潜在选民,所以他们自然选择了获取更多选民的方式。
团结美国需要让众多那些不支持拜登,支持特朗普的人变为支持拜登。可是,拜登为了吸引这些民众所提出的模仿特朗普的政策总比不上特朗普的政策,在未能让特朗普支持者增加拜登倾向的情况下怎么能够转变他们的支持对象呢?
如果民众在各种议题上的观点不能够有着较为一致的意见,继续保持着这种巨大的割裂,拜登以及任何总统都不能够团结美国。